One of today's greatest global energy challenges is the need for more affordable, reliable, clean, secure and renewable sources of electricity. Currently, we rely heavily on coal, oil, natural gas and nuclear fuels to generate electricity. The 2018 BP Statistical Review of World Energy shows fossil fuels (oil, gas, coal and nuclear) still account for about 90% of global primary energy consumption while renewable power hit a new high of 3.6%.

 

Fossil fuels are not renewable. Their resources are limited and will eventually diminish and become more expensive. Their mining, transportation and combustion generate air emissions, acid rain, water pollution, and, most detrimentally, CO₂ emissions that are the primary greenhouse gas contributing to recent climate change. Nuclear energy is cheap and clean without adding greenhouse gases to the atmosphere, but the disposal of radioactive waste produced from the nuclear power generation is an ongoing problem. Producing energy from these resources impacts on our environment, polluting our air, land, and water. In contrast, many types of renewable energy sources are replenishable and will never run out.

 

Wind power is a commercially proven, rapidly growing form of electricity generation that provides clean, renewable, and cost-effective electricity around the world. Some countries (Germany, Demark, Spain) have supported wind industry heavily since the end of the twentieth century. Recently, China and India have started to invest more in wind energy development and have showed the highest growing rates of wind energy installed power in the past years.

 

Wind turbine performance can be described by Betz's theory. It was first introduced by a German physicist, Albert Betz, in 1919. The theory states the maximum power able to be generated from wind is independent of the turbine design. By the conservation of energy and conservation of mass, wind turbines can extract energy by slowing down the incoming wind. If a wind turbine wants to be 100% efficiency, the rotor would have to stop 100% of the wind and the wind speed behind the rotor would be zero. In other words, the rotor would need to be a solid disk and the wind would pile up in front of the rotor and the air flows around it instead of passing through it. The rotor would not turn and no kinetic energy would be converted.

 

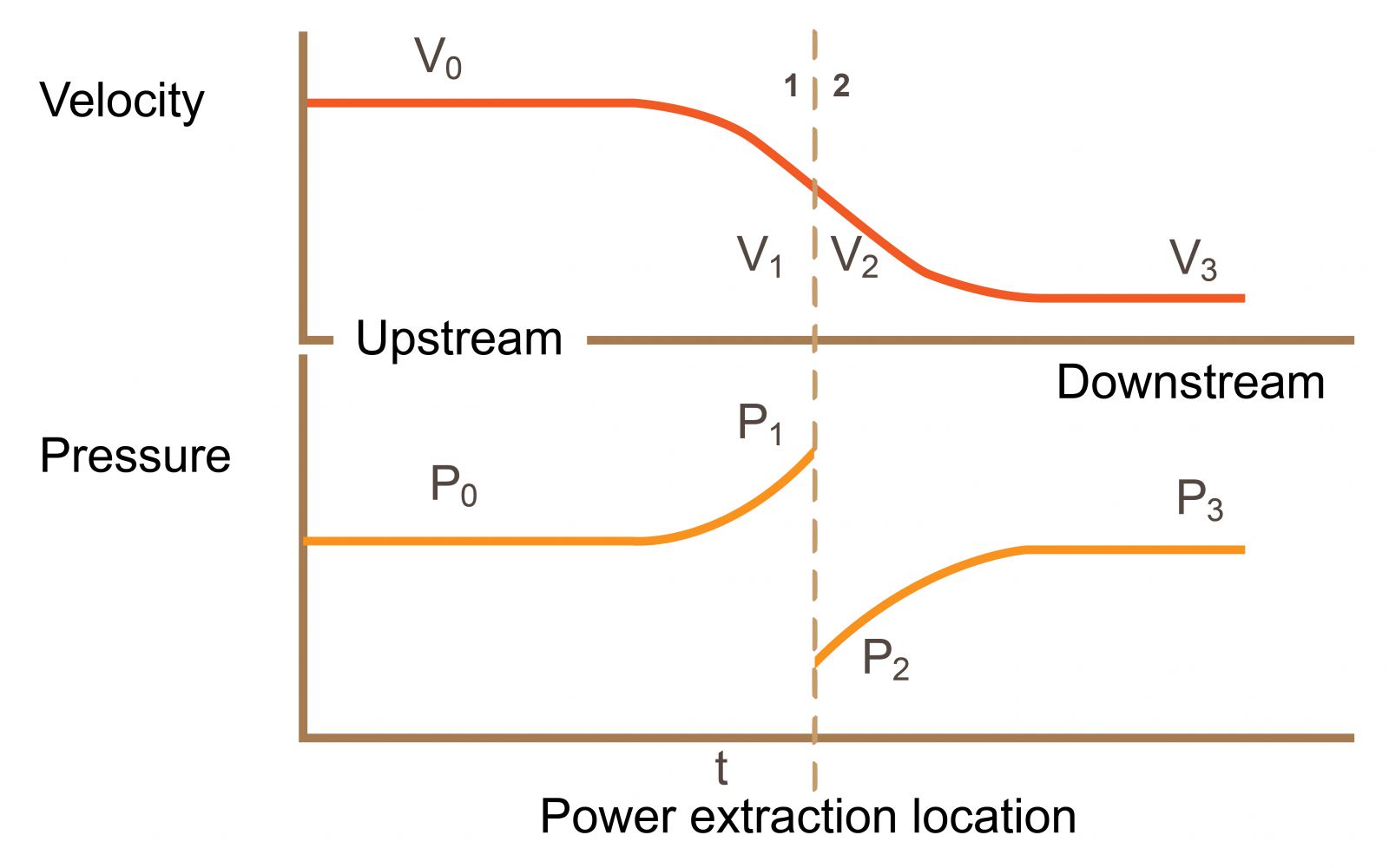
Consider a rotor, which does not possess a hub, in a steady and uniform wind field and assume the rotor extracts a fraction of the extreme kinetic energy from the wind. The downstream wind speed will be smaller than the upstream wind speed (V₃ < V₀). Thus, according to the conservation of mass, the cross section area of the upstream should be smaller than the downstream (A₀ < A₃). A control surface corresponding to a set of streamlines bounds a controlled volume and there is no flow crossing the surface. The air is assumed to be non-compressible and the density remains constant, and there is no heat transfer. The volumetric flow rate, Q, is

 

Q = V₀A₀ = V₃A₃ = VA

 

where V₀ is the wind speed in the front of the rotor, V₃ is the wind speed downstream of the rotor and V is the wind speed by the rotor, A₀ and A₃ are the area of the wind before and after reaching the rotor while A is the area at the rotor.

Bernoulli equation cannot be applied here because the energy loss occurs at the rotor location. Hence, Bernoulli equation can be applied before the rotor, from pressure P₀ to P₁, and also after the rotor, from pressure P₂ to P₀, individually.

 

before the rotor P₀/ρ+(1/2)V₀² = P₁/ρ+(1/2 )V²

 

after the rotor P₂/ρ+(1/2)V² = P₀/ρ+(1/2)V₃²

 

The pressure drop by the rotor can be expressed as

 

P₁/ρ-P₂/ρ = ( P₀/ρ+(1/2)V₀² )-( P₀/ρ+(1/2)V₃² )  .

 

So, P₁-P₂ = (1/2)ρ(V₀²-V₃²).

 

The figure below shows the schematics of the velocity and pressure variation before and after the rotor.

 

Wind Turbine Power: The Betz Limit and Beyond by Mahmoud Huleihil

 

The pressure drop induced by the rotor is directly proportional to the axial thrust (T) exerted by the flow on the rotor and is equal to the deficit in the momentum flux from the upstream to the downstream area.

 

T = (1/2)Aρ(V₀²-V₃² ) = ρQ(V₀-V₃)

 

The wind speed by the rotor is the average of the upstream and the downstream velocities, given as

 

V = 1/2 (V₀+V₃)

 

Now consider the kinetic power extracted by the turbine. It is the kinetic energy difference between the upstream and the downstream. Kinetic power at one location can be expressed as

 

E = Q(1/2)ρV² = 1/2 ρAV³

 

Power extracted by the rotor is

 

∆E = (1/2)ρQ(V₀²-V₃² ) = (1/2)ρAV(V₀²-V₃² )

 

To calculate the turbine efficiency, Betz suggests to divide the power extracted at the rotor by a reference power. The power coefficient (C_p) is the ratio of the power generated by turbine over the reference power. The reference power is the power of air upstream moving at V₀ contained in a cylinder with the area of the rotor (A).

 

C_p = ∆E/E_ref  = ∆E/((1/2)ρAV₀³)

 

Because C_p only depends on the upstream and the downstream velocities (V₀ and V₃), 

the power coefficient (C_p) can be rewritten as

 

C_p=((1/2)ρAV(V₀²-V₃² ))/((1/2)ρAV₀³ ) = (1/2(V₀+V₃)(V₀²-V₃² ))/V₀³ 

 

Substituting a = V₃/V₀ ,

 

C_p = 1/2(1+a)(1-a² )

a_max = 1/3

⁡(C_p)_max = 16/27 ≈ 0.5926

 

The maximum power that could be extracted from a wind stream is:

 

P_max = ∆E = C_p(1/2)ρAV₀³ = (16/27)(1/2)ρAV₀³

 

 

 

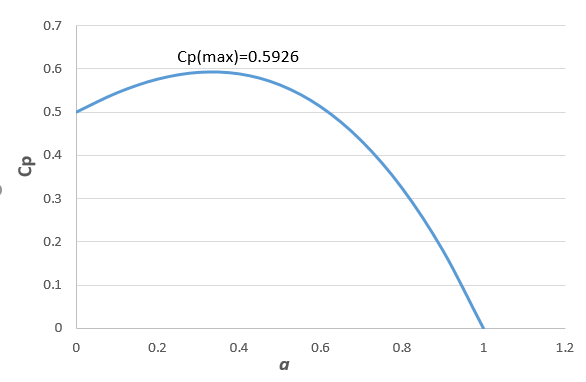
Note that the horizontal axis reflects the ratio, a = V₃/V₀, the vertical axis is the power coefficient, C_p, in the figure above.

 

The power coefficient reaches a maximum value of 0.5926 when a is equal to one third. This is referred to be as the Betz's Limit. This theoretical value means that no turbine can capture more than 16/27 of the kinetic energy of the upstream wind when the outlet velocity is equal to one-third the wind speed. Therefore, the larger area at the downstream is needed for the kinetic energy to be conserved. This is the ideal situation and viscous of turbulent dissipation is neglected. 

 

However, modern wind turbines can achieve peak values of C_p in the range of 0.45 to 0.50 which is about 75% to 85% of the theoretically value. After taking into account other ineffiencies in a complete wind turbine system, e.g. the generator, blade surface roughness, power transmission and other mechanical imperfections, only 20-40% of the wind power is actually converted into usable electricity.